Euclide (C. 330-275 BCE, fl. vers 300 avant notre ère)

qui est Euclide

Le mathématicien grec Euclide a vécu et prospéré à Alexandrie en Egypte vers 300 avant notre ère, sous le règne de Ptolémée Ier., On ne sait presque rien de sa vie, et aucune ressemblance ou description de première main de son apparence physique n’a survécu à l’Antiquité, et donc les représentations de lui (avec une longue barbe et une casquette en tissu) dans les œuvres d’art sont nécessairement le produit de l’imagination de l’artiste.

Il a probablement étudié un temps à L’Académie de Platon à Athènes mais, à L’époque D’Euclide, Alexandrie, sous le patronage des Ptolémées et avec sa bibliothèque prestigieuse et complète, était déjà devenue un digne rival de la grande académie.,

Euclide est souvent appelé le « père de la géométrie”, et il a peut-être écrit le manuel mathématique le plus important et le plus réussi de tous les temps, le « Stoicheion” ou « éléments”, qui représente l’aboutissement de la révolution mathématique qui avait eu lieu en Grèce jusqu’à cette époque., Il a également écrit des travaux sur la division des figures géométriques en parties dans des rapports donnés, sur la Catoptrique (la théorie mathématique des miroirs et de la réflexion), et sur l’astronomie sphérique (la détermination de l’emplacement des objets sur la « sphère céleste”), ainsi que des textes importants sur l’optique et la musique.,

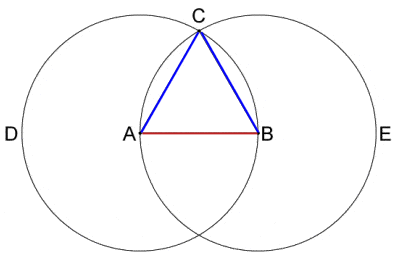
La méthode D’Euclide pour construire un triangle équilatéral à partir D’un segment de droite AB donné en utilisant seulement une boussole et un bord droit était la Proposition 1 dans le livre 1 des « éléments”

Les « éléments” était une compilation lucide et complète et une explication theudius, theaetetus et eudoxus. En tout, il contient 465 théorèmes et preuves, décrits dans un style clair, logique et élégant, et utilisant seulement une boussole et un bord droit., Euclide a retravaillé les concepts mathématiques de ses prédécesseurs en un tout cohérent, plus tard pour devenir connu sous le nom de géométrie euclidienne, qui est toujours aussi valable aujourd’hui qu’il y a 2 300 ans, même dans les mathématiques supérieures traitant des espaces de dimension supérieure. Ce n’est qu’avec les travaux de Bolyai, Lobachevski et Riemann dans la première moitié du 19ème siècle que tout type de géométrie non euclidienne a même été envisagé.,

Les « éléments” sont restés le manuel définitif sur la géométrie et les mathématiques pendant plus de deux millénaires, survivant à l’éclipse dans l’apprentissage classique en Europe pendant les âges sombres grâce à des traductions arabes. Il a établi, pour tous les temps, le modèle de l’argument mathématique, en suivant des déductions logiques des hypothèses initiales (Qu’Euclide a appelées « axiomes” et « postulats ») afin d’établir des théorèmes éprouvés.

les cinq axiomes généraux D’Euclide étaient:

1. Les choses qui sont égales à la même chose sont égales les unes aux autres.,
2. Si des égaux sont ajoutés à des égaux, les entiers (sommes) sont égaux.
3. Si les égaux sont soustraits des égaux, les restes (différences) sont égaux.
4. Les choses qui coïncident les unes avec les autres sont égales les unes aux autres.
5. Le tout est supérieur à la partie.

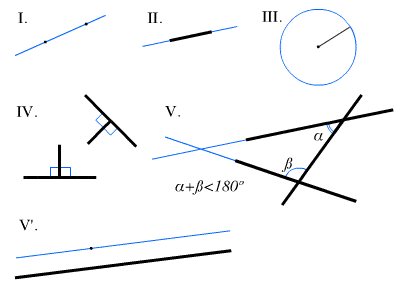
Euclide Postulats de (1 – 5)

Ses cinq géométrique postulats ont été:

1. Il est possible de tracer une ligne droite à partir de n’importe quel point à n’importe quel point.
2. Il est possible d’étendre une ligne droite finie en continu dans une ligne droite (c’est-à-dire, un segment de ligne peut être étendu au-delà de l’un de ses points d’extrémité pour former un segment de ligne arbitrairement grand).
3. Il est possible de créer un cercle avec n’importe quel centre et distance (rayon).
4. tous les angles droits sont égaux les uns aux autres (c’est-à-dire « la moitié” d’un angle droit).
5. si une ligne droite traversant deux lignes droites rend les angles intérieurs d’un même côté inférieurs à deux angles droits, les deux lignes droites, si elles sont produites indéfiniment, se rencontrent du côté sur lequel les angles sont inférieurs aux deux angles droits.,iv>

   partie de la preuve D’Euclide du théorème de Pythagore

   parmi beaucoup d’autres joyaux mathématiques, les treize volumes des « éléments” contiennent des formules pour calculer les volumes de solides tels que les cônes, les pyramides et les cylindres; des preuves sur les séries géométriques, les nombres parfaits et les nombres premiers; des algorithmes pour trouver le plus grand preuve définitive qu’il ne peut y avoir que cinq solides platoniques réguliers possibles.,

   cependant, les « éléments” comprennent également une série de théorèmes sur les propriétés des nombres et des entiers, marquant les premiers débuts réels de la théorie des nombres. Par exemple, Euclide a prouvé ce qui est devenu connu comme le théorème fondamental de L’arithmétique (ou le théorème Unique de factorisation), que tout entier positif supérieur à 1 peut être écrit comme un produit de nombres premiers (ou est lui-même un nombre premier). Ainsi, par exemple: 21 = 3 x 7; 113 = 1 x 113; de 1 200 = 2 x 2 x 2 x 2 x 3 x 5 x 5; 6,936 = 2 x 2 x 2 x 3 x 17 x 17; etc., Sa preuve était le premier exemple connu d’une preuve par contradiction (où tout contre-exemple, qui autrement prouverait une idée fausse, est montré pour n’a aucun sens logique lui-même).

   Il a été le premier à réaliser et de prouver qu’il existe une infinité de nombres premiers. La base de sa preuve, souvent connue sous le nom de Théorème D’Euclide, est que, pour tout ensemble donné (fini) de nombres premiers, si vous les multipliez tous ensemble puis en ajoutez un, alors un nouveau nombre premier a été ajouté à l’ensemble (par exemple, 2 x 3 x 5 = 30, et 30 + 1 = 31, un nombre premier) un processus,

   bien que les Pythagoriciens aient pu connaître le nombre D’Or (φ, approximativement égal à 1,618), Euclide a été le premier à le définir en termes de rapports (AB:AC = AC:CB), et a démontré son apparence dans de nombreuses formes géométriques.,

   << Back to Hellenistic Mathematics

   Forward to Archimedes >>